The concept of average speed is introduced in the school from the 8th or 9th standard. Apart from this, it is also asked in the quantitative aptitude or the numerical section of the various competitive exams such as IBPS PO, IBPS Clerk, NDA, SSC CGL etc. However, to understand the average speed formula, the students need to understand the concept of speed and why it doesn't work as a regular average.
The average speed is an important component in determining how long it takes to finish a journey. Average speed is a method that calculates the rate of travel time and distance. The fact that the speed changes throughout the journey emphasise the need to determine the average speed. There are various methods for determining an object's or vehicle's average speed.
However, it seems that the topic is simpler enough to comprehend, but somehow the rules of your regular averages don't apply. Therefore, the term "Average" becomes confusing.
During school time, we learnt the below formula for average:
Average = (Sum of entities)/ (Number of entities)
However, the Average Speed is not the same as the average of all speeds. So, how do we figure it out? Let's take a look.
Average Speed Definition
It mainly combines two words and two ideas that are "Average" and "Speed". The term average is mainly obtained from the individual data points, and the speed is mainly the change in position.
If you can time the motion and measure the distance, you can easily calculate the average speed.
In simple terms, Average Speed can be defined as the total distance covered by the object at a particular time interval. It is a scalar quantity, which means it doesn't have a direction. It is mainly represented by the magnitude.
The average speed of a body during a period of time is its mean value. Because the speed of a moving body is not constant and fluctuates over time, therefore the formula for average speed is required. Even with changing speed, the total time and total distance traversed may be employed. We can get a single value to describe the complete motion using the average speed calculation.
Know the Average Speed Formula
The average speed formula is equal to the total distance covered by the object in a question divided by the total time taken by the object to travel the distance, i.e., the total period of time.
Average Speed Formula:
If an object covers x1,x2,x3,x4……… t1,t2,t3,t4 ... .. time respectively then:
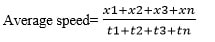
Let’s understand this using a problem, suppose a truck travels S1 mph at time t1 on a trip and S2 mph at time t2 on a return trip. Find out the average speed of the truck during the entire trip?
For this type of problem, don't add the 2 speeds even if the time is the same. This will NOT give you.
Let’s find the answer,
Total average speed = total distance/ total time taken
i.e, Average Speed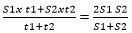 
Instantaneous Speed:
Average speed include the events such as an acceleration of a car from the stop, travelling for a while, speeding up, then slowing down at the yellow light and stops.
An automobile moves at various speeds. The automobile is not moving at 55 mph at any one time. Miles per hour (mph). It may be 0 mph one moment, 8 mph the next, 53 mph the next, 60 mph the next, and eventually 5 mph before reverting to 0 mph.
You use the average speed of all the discrete occurrences, like the automobile went 5.5 miles in 6 minutes, to simplify measurements and make progress on a physics or maths topic.
In several cases, there is no need to know the instantaneous speed formula, v finds the limit with changes in time (instant) and approaches “0”:
Throughout a timed event, instantaneous speeds change. Estimating average speed is far easier — and often more informative – than calculating instantaneous speed.
Average Speed Formula in Some Special Cases
Case 1: The formula for average speed is provided below for a body or object travelling at a speed of S1 for time t1 and speed S2 for time t2. The lengths traversed in time periods and are calculated as the product of S1 x t1 and S2 x t2 correspondingly.
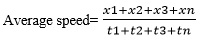
Case 2: When 'n' various speeds, S1, S2, S3,... Sn, are supplied for 'n' different individual time periods, t1, t2, t3,...tn, the average speed formula is:
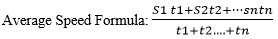
Case 3: When different distances d1, d2,..... dn are covered in a different interval of time t1, t2 …tn, respectively:
Procedure to Calculate Average Speed
To determine the average speed, you must know the total distance covered by an object and the total time taken by the object to cover the journey.
The triangle's three parts are geometrically aligned in the right positions:
Divide total distance by elapsed time to get average speed, s: D x t
Divide total distance by speed to get elapsed time, t: D x s
Multiply speed by the length of time to get distance, D: s x t
For example: If you want to find the average speed of a car that covers the distance of 82.6 km in 2 hours.
Put these two numbers in the triangle and get 41.3 km per hour.
Find Average Speed
For example: If you want to find the average speed of a car that covers the distance of 82.6 km in 2 hours.
Put these two numbers in the triangle and get 41.3 km per hour.
Find Total Distance
To find the total distance, you must have speed and time;
D= 41.3km/h x 2 hours
= 82.6km
Solved Examples of Average Speed
- A bus travels at a 200 km/hr speed for 1 hour and then slows down to 120 km/hr for the next 1 hour. Find the average speed of the bus.
- Rajat drove for 1 hour at 50mph and 3 hours at 60 mph in travelling from Delhi to Goa. What was his average speed during the entire journey?
Solution: Distance= Speed x Time
So, distance covered in one hour = 50 x 1= 50 miles.
Distance covered in next 3 hours= 60 x 3= 180 miles
Total Distance covered: 50+180 miles= 230 miles
Total time taken: 1+3= 4 hours
= 230/4 = 57.5 mph
Practice Questions on Average Speed
- For the first 4 hours, a train is moving at the speed of 80 km/h and 110 km/hr for the next 3 hours. Find the average speed of the train.
- A fox can cover 0.6 miles in 36 seconds. Find out the average speed of the fox miles per second and also find the speed in miles per hour ( multiply by 3600)
Solve the average speed questions that can be difficult for the students as this topic include not only in the maths subject but in the physics of higher classes. If you are facing difficulties in solving the equation, then join our online physics class to clear your doubts at once. The following are the benefits you can avail of:
- Live one-on-one interactive sessions
- Unlimited doubt clearing sessions and revision classes
- 24*7 student support
- Affordable fee structure
