Here’s All About Integrated Rate Equation

A differential rate equation describes how the rate of a chemical reaction depends on the concentrations of the reactants. The instantaneous rate of reaction at any moment can be determined as the slope of the tangent line on a concentration-time graph. However, directly calculating the rate of reaction from such graphs is challenging. To address this, we integrate the differential rate equation to derive a relationship between concentration at various times and the rate constant. This integrated form of the rate equation allows for easier analysis of the reaction's progress over time.

The integrated rate equation varies depending on the order of the reaction. For each reaction order, the mathematical expression linking concentration and time takes a different form, which helps in characterizing the reaction's kinetics. By using the integrated rate equations, we can predict the concentration of reactants at any given point in time, making it easier to understand the reaction's behavior and to determine important parameters like the rate constant. Each reaction order—whether zero, first, or second—has its specific integrated rate law, and identifying the correct one is essential for accurate analysis and understanding of the reaction mechanism.

Zero order reaction:

In a zero-order reaction, the rate remains constant and independent of reactant concentration, as the rate depends on the zeroth power of the concentration. This means that the reaction rate is unaffected by changes in reactant concentration. Zero-order reactions are rare but occur under specific conditions, like the thermal decomposition of hydrogen iodide (HI) on a gold surface or ammonia decomposition on a hot platinum surface. The rate constant, k, governs the reaction rate, which stays steady over time. Integrated rate law equations for zero-order reactions offer insights into chemical kinetics when reactant concentration does not influence the rate.

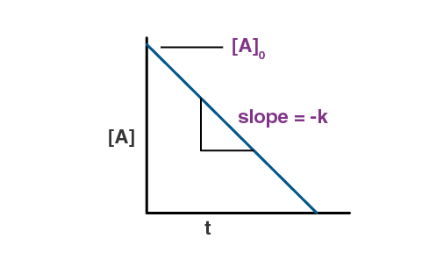
Integrated rate equation for zero order reaction:

This can be represented as a straight line when plotted with the reactant concentration on the y-axis and time (t) on the x-axis. In this plot, the slope of the straight line corresponds to the rate constant, k, and this relationship makes it straightforward to determine the rate constant from experimental data. Since the reaction rate is constant for zero-order reactions, the concentration decreases linearly over time, and the rate of reaction is unaffected by the concentration of the reactant. The linearity of the plot allows for easy identification of key parameters, such as the rate constant, by simply calculating the slope. This graphical method provides valuable insights into the kinetics of zero-order reactions, helping researchers understand how the reaction progresses over time and offering a clear way to analyze the rate of reaction through experimental data.

First order reaction:

In a first-order reaction, the rate depends on the concentration of the reactants raised to the first power. Examples of first-order reactions include the natural and artificial radioactive decay of unstable nuclei. These reactions follow a specific pattern where the rate of reaction is directly proportional to the concentration of the reactant. The general equation for a first-order reaction, which includes the rate constant k, is derived based on this relationship. The derived integrated rate equation for first order reaction is useful for analyzing and predicting the behavior of first-order reactions in various contexts, such as nuclear decay and certain chemical processes.

A → B

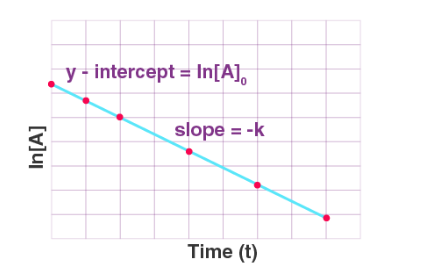
The equation for a first-order reaction can be represented as a straight line when plotted with ln[A] (the natural logarithm of the concentration) on the y-axis and time (t) on the x-axis. In this plot, the slope of the line is negative, and its value is directly related to the rate constant, k. The linear nature of this relationship makes it simple to determine the rate constant from experimental data. By calculating the negative slope of the line, we can easily find the value of k, which gives us valuable information about the reaction’s rate. This approach allows for a clear understanding of how the concentration of reactants changes over time, providing insights into the kinetics and overall behavior of the reaction. The ability to calculate k from experimental data through a linear plot helps researchers predict and analyze the reaction's progress and the factors affecting its rate.

We can also determine the value of the rate constant, k from the equation as:

Integrated rate equation for first order reaction:

By using the integrated rate equation for first order reaction and zero-order reactions, we can calculate the concentration and rate of reaction at any given time. These equations provide a way to relate concentration changes over time to the reaction rate. For zero-order reactions, the relationship is linear with concentration, while for first-order reactions, the natural logarithm of the concentration is plotted against time. In both cases, these integrated equations allow us to analyze the reaction's progress and determine important parameters like the rate constant, providing a clear understanding of the reaction kinetics.

Second Order Reaction

Second-order reactions are chemical reactions where the total sum of the exponents to which the concentration terms in the rate law are raised is on the order of two.

The rate of such reaction is given as-

It is possible to determine from these integrated rate equations for second order reactions that they have either a concentration of one second order reactant or two first order reactants.

Let us see some examples –

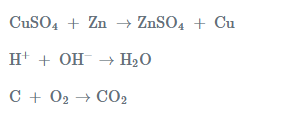
Examine the reactant concentrations in the examples provided. One thing you notice is that the concentrations of the reactants add up to two, and they are of the first order. According to the reactivity series, these reactions are second-order.

Conclusion

In conclusion, integrated rate equations are essential tools for understanding and analyzing chemical reactions. By integrating the differential rate equation, we can relate the concentration of reactants to time and determine important parameters like the rate constant. For zero-order reactions, the relationship between concentration and time is linear, while for first-order reactions, the natural logarithm of concentration is plotted against time. These equations enable the prediction of reaction behavior and the calculation of concentrations at any moment. By applying these principles taught in Online Tuition Classes, we can gain valuable insights into the kinetics and mechanisms of chemical reactions.