Understanding Angular Momentum: Dimensions and Formulas

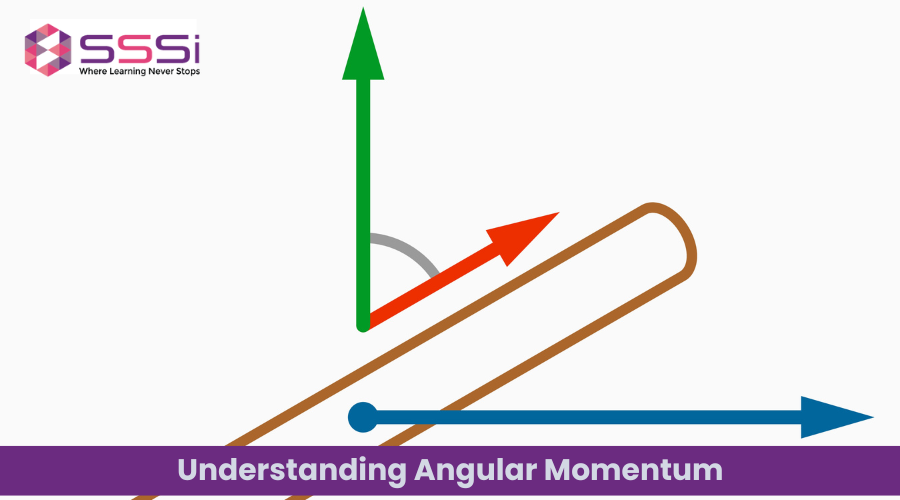
The basic concept in classical mechanics that describes the rotational motion of an object is known as angular momentum, which has a great deal to do with understanding how an object behaves under forces causing it to rotate and is therefore of great importance in the fields of physics, engineering, and even astrophysics. One of the more important aspects of angular momentum has to do with dimensional analysis which helps understand its physical quantities about how they might be related, in terms of basic units, to one another. Below we will look into the angular momentum dimensions, and its formula, and relate it to the other quantities of angular velocity and momentum. We will also discuss how online tuition classes can help students understand these concepts better.

What is Angular Momentum?

A measure of the moment of inertia or rotational inertia that describes the properties of an object in motion and its tendency around a specific axis is called the angular momentum vector quantity. It can best be understood from an analogy made with linear momentum, but if linear momentum expresses the motion along a straight path, then here it revolves around a certain point or the axis. Hence, the equation for the angular momentum of a particle is given as: L=r×p

Where:

• r is the position vector of the particle relative to the axis of rotation
• p is the linear momentum of the particle, and
• × is the cross product between the two vectors.

The angular momentum of a rigid body rotating about a fixed axis is given by the expression:

L=I⋅ω

Where:

• “I” is the moment of inertia of the object, and
• ω is the angular velocity of the object.

Both these measures have an angular momentum quantifying the extent of rotation for the object in question. Its magnitude is both a function of the distribution of mass for the object in question and of the rotational velocity.

Dimensional Formula of Angular Momentum

We see the dimensional formula of angular momentum to understand the physical meaning of it. The dimensional formula is a relation between angular momentum and fundamental quantities like mass, length, time, and other physical dimensions. For a particle, the formula for angular momentum is derived from its definition as follows:

L = r × p

Where:

r has the dimension of length ([L]),

p has the dimension of momentum ([MLT−1])

Hence, the dimensional form of angular momentum is:

[L]=[r×p]=[L]×[MLT−1]=[ML^2T−1]

 where;

• M is the mass
• L is length, and
• T is time,

Thus, the above equations, depict that angular momentum has the quantity of mass which is multiplied by the square of length and finally divided by the time.

Dimension of Angular Momentum in Terms of Other Quantities

The dimension of angular momentum can be studied in terms of its relationship with other quantities. Angular momentum depends on the product of the moment of inertia (I) and angular velocity ω.

The moment of inertia I, for a particle of mass m located at a distance r from the axis of rotation is defined as I=mr2. Its dimensional formula is [I] = [ML^2]

The angular velocity is defined as the rate of change of angular displacement and has the dimensional formula as follows: [ω]=[T^-1]

Therefore, the dimension of angular momentum can also be expressed as:

L=I⋅ω⇒[L]=[ML^2]⋅[T−1]=[ML^2T^−1]

This verifies that the dimension of angular momentum is actually.

Momentum Dimensional Formula and Its Connection with Angular Momentum

As a vector quantity, momentum is the product of the mass of an object and its velocity. In mathematical terms, it can be represented as: p=mv

The dimensional formula for momentum is: [p]=[M][LT^−1]=[MLT^−1]

While angular and linear momenta share the same basis factors, mass and motion, their quantities are different because the direction of motion is different. Linear momentum is about motion along a straight line, whereas angular momentum is about rotation around an axis. Though they are different, both are related through cross-product position and velocity or linear momentum, as shown above.

It should be remembered that angular momentum is always a vector quantity whereas momentum is linear and therefore can be specified in one dimension.

Dimensional Formula of Angular Velocity

Angular velocity, symbolised by ω, represents the rate of rotation of any object around an axis. This is defined as the rate of change of angular displacement with time:

dθ/dt= Δω=Δ θ/Δ t

Here,

θ represents angular displacement,

t is the time.

Thus, the dimensional representation of angular velocity is: [ω]=[T^−1]

This indicates that angular velocity is the rate of change of angular position and therefore has the dimension of inverse time.

How Online Tuition Classes Help in Understanding These Concepts

To understand complexities in angular momentum, dimensional analysis, and their related topics comprehensively, usually, students usually consider seeking external resource support. Since online tuition classes are a rather convenient and highly effective way by which students can seek knowledge about their concepts from the comfort of their houses, they remain effective study aids.

The use of online tuition allows students to have interactive lessons on the basics and advanced topics of angular momentum. The tutors can provide personal explanations of the dimensional formula of angular momentum and take students through step-by-step calculations to ensure that the students clearly understand how to derive and apply the momentum dimensional formula in different situations.

Online learning platforms usually include visual aids, simulations, and quizzes to help students understand abstract concepts like angular velocity and its relationship with other physical quantities. Since a student can rewind lessons and ask questions at will, they can learn at their own pace, which makes online tuition an invaluable tool for mastering the intricacies of angular momentum and its dimensions.

Conclusion

Angular momentum is another very important term in rotational dynamics. Students from physics and engineering need to have an understanding of its dimensional formula and related terms like angular velocity and momentum. Angular momentum dimensions explain how things work in this world under a state of rotation, bringing out mass, length, and time into order. This helps the student understand the true nature of the concept of angular momentum and place it in proper perspective within a broader framework of mechanics.

Online tuition classes present the ability and effectiveness of flexible learning to students who want more education about these complicated subjects. As a result, students will be able to learn angular momentum, dimensional analysis, and rotational dynamics with a much better understanding in class and tend to perform better on tests.